某种家用电器每台的销售利润与该电器的无故障时间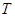 (单位:年)有关,若
(单位:年)有关,若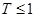 ,则销售利润为0元;若
,则销售利润为0元;若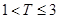 ,则销售利润为100元,若
,则销售利润为100元,若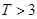 ,则销售利润为200元.设每台该种电器的无故障使用时间
,则销售利润为200元.设每台该种电器的无故障使用时间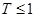 ,
,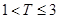 ,
,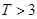 这三种情况发生的概率分别为
这三种情况发生的概率分别为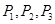 ,又知
,又知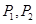 为方程
为方程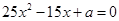 的两根,且
的两根,且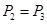 .
.
(1)求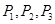 的值;
的值;
(2)记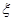 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求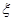 的分布列及数学期望.
的分布列及数学期望.
推荐套卷
某种家用电器每台的销售利润与该电器的无故障时间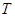 (单位:年)有关,若
(单位:年)有关,若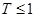 ,则销售利润为0元;若
,则销售利润为0元;若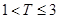 ,则销售利润为100元,若
,则销售利润为100元,若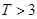 ,则销售利润为200元.设每台该种电器的无故障使用时间
,则销售利润为200元.设每台该种电器的无故障使用时间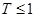 ,
,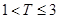 ,
,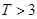 这三种情况发生的概率分别为
这三种情况发生的概率分别为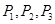 ,又知
,又知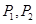 为方程
为方程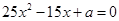 的两根,且
的两根,且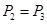 .
.
(1)求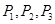 的值;
的值;
(2)记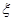 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求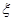 的分布列及数学期望.
的分布列及数学期望.