设某大学的女生体重 (单位:kg)与身高
(单位:kg)与身高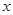 (单位:cm)具有线性相关关系,根据一组样本数据(
(单位:cm)具有线性相关关系,根据一组样本数据(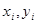 )(
)(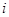 =1,2,…,n),用最小二乘法建立的回归方程为
=1,2,…,n),用最小二乘法建立的回归方程为 =0.85
=0.85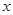 —85.71,则下列结论其中正确的个数是( )
—85.71,则下列结论其中正确的个数是( )
① y与x具有负的线性相关关系
② 回归直线过样本点的中心( ,
,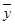 )
)
③ 若该大学某女生身高增加1cm,则其体重约增加0.85kg
④ 若该大学某女生身高为170cm,则可断定其体重必为58.79kg
| A.0 | B.1 | C. 2 | D. 3 |
推荐套卷
设某大学的女生体重 (单位:kg)与身高
(单位:kg)与身高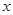 (单位:cm)具有线性相关关系,根据一组样本数据(
(单位:cm)具有线性相关关系,根据一组样本数据(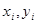 )(
)(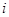 =1,2,…,n),用最小二乘法建立的回归方程为
=1,2,…,n),用最小二乘法建立的回归方程为 =0.85
=0.85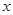 —85.71,则下列结论其中正确的个数是( )
—85.71,则下列结论其中正确的个数是( )
① y与x具有负的线性相关关系
② 回归直线过样本点的中心( ,
,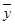 )
)
③ 若该大学某女生身高增加1cm,则其体重约增加0.85kg
④ 若该大学某女生身高为170cm,则可断定其体重必为58.79kg
| A.0 | B.1 | C. 2 | D. 3 |