某商场有奖销售中，购满100元商品得一张奖券,多购多得,1000张奖券为一个开奖单位,特等奖1个,等奖10个,等奖50个.一张奖券中特等奖、一等奖、二等奖的事件分别为A、B、C,求:
(1)
,
,
;
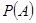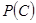(2)1张奖券的中奖概率；
(3)1张奖券不中特等奖且不中一等奖的概率.
相关试题
。
时，求曲线
在
处切线的斜率；
的单调区间；
时，求
上的最小值。
满足
。
的解析式；
的值域。
是公差为－2的等差数列，
是
与
的等比中项。
，求
。
；
，求实数a的取值范围。
，设曲线
在点
处的切线为
。
的值；
，其中
。
时，
。推荐套卷
某商场有奖销售中，购满100元商品得一张奖券,多购多得,1000张奖券为一个开奖单位,特等奖1个,等奖10个,等奖50个.一张奖券中特等奖、一等奖、二等奖的事件分别为A、B、C,求:
(1),,;
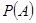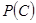(2)1张奖券的中奖概率；
(3)1张奖券不中特等奖且不中一等奖的概率.
粤公网安备 44130202000953号