已知双曲线
与椭圆
有相同的焦点，点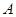
、
分别是椭圆的右、右顶点，若椭圆经过点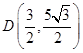
．
（1）求椭圆的方程；
（2）已知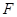
是椭圆的右焦点，以
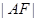为直径的圆记为
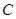，过点
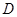引圆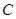的切线，求此切线的方程；
（3）设
为直线
上的点，
是圆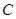上的任意一点，是否存在定点
，使得
？若存在，求出定点的坐标；若不存在，说明理由．
相关试题
；
，且
，求
的值．
在区间
上的图像（完成列表并作图）。
、
、
是同一平面内的三个向量，其中
，且
，求
，且
与
垂直，求
与
的夹角
．
中，
分别是
的中点，
为交点，若
=
，
=
，
、
、
．
，
．
的最小正周期和单调递减区间；
中的三个内角
所对的边分别为
，若锐角
满足
，且
，
，求
,
，且
的夹角是
，三角形ABC的面积
，求a+b.推荐套卷
已知双曲线与椭圆有相同的焦点，点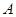、分别是椭圆的右、右顶点，若椭圆经过点．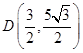
（1）求椭圆的方程；
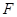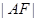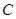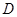（2）已知是椭圆的右焦点，以为直径的圆记为，过点引圆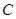的切线，求此切线的方程；
（3）设为直线上的点，是圆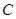上的任意一点，是否存在定点，使得？若存在，求出定点的坐标；若不存在，说明理由．
粤公网安备 44130202000953号