（本小题满分12分）
如图，在三棱锥D－ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB＝BC＝a，E为BC的中点，F在棱AC上，且AF＝3FC．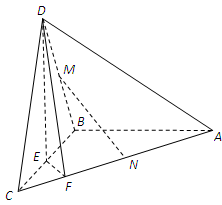
（1）求三棱锥D－ABC的表面积；
（2）求证AC⊥平面DEF；
（3）若M为BD的中点，问AC上是否存在一点N，使MN∥平面DEF？若存在，说明点N的位置；若不存在，试说明理由．
相关试题
（本小题满分12分）如图，正三棱柱ABC—A1B1C1中，D是BC的中点，AA1=AB=1.
（I）求证：A1C//平面AB1D；
（II）求二面角B—AB1—D的大小；
（III）求点C到平面AB1D的距离.
已知直四棱柱ABCD—A′B′C′D′的底面是菱形，
，E、F分别是棱CC′与BB′上的点，且EC=BC=2FB=2.
（1）求证：平面AEF⊥平面AA′C′C；
（2）求截面AEF与底面ABCD所成二面角的大小.
是定义在
上的增函数，且对一切
满足
.
的值;
解不等式
.
中，
，
将
沿
折起到
的位置，使平面
平面
； 
的侧面积.
的侧面
是菱形，
平面
；
是
上的点，且
平面
，求
的值.推荐套卷
粤公网安备 44130202000953号