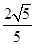在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,D、E、F分别是棱AB、BC、CP的中点,AB=AC=1,PA=2,则直线PA与平面DEF所成角的正弦值为( )
A. 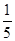 B.
B. 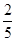 C.
C. 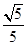 D.
D. 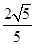
推荐套卷
在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,D、E、F分别是棱AB、BC、CP的中点,AB=AC=1,PA=2,则直线PA与平面DEF所成角的正弦值为( )
A. 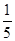 B.
B. 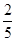 C.
C. 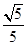 D.
D.