(10分)一根长为l的线，一端固定，另一端悬挂一个小球，如图．已知小球从M点放下，经过0.5秒第一次到达平衡位置O.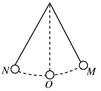
(1)求小球第三次经过平衡位置O的时间．
(2)求小球运动的周期．
(3)经过7.2秒，小球是在平衡位置的右边还是左边？
与曲线
有相同的焦点。
且
的双曲线的标准方程。
与双曲线
的左支交于
两点，另一直线
过点
和
的中点，求直线
轴上的截距
的取值范围。
到点
的距离之差为
，到
轴的距离与到
轴的距离之比为
，求
的取值范围。
的双曲线与椭圆
有相同焦点，求双曲线的方程。推荐套卷
(10分)一根长为l的线，一端固定，另一端悬挂一个小球，如图．已知小球从M点放下，经过0.5秒第一次到达平衡位置O.
(1)求小球第三次经过平衡位置O的时间．
(2)求小球运动的周期．
(3)经过7.2秒，小球是在平衡位置的右边还是左边？
粤公网安备 44130202000953号