在直角坐标系
中，点
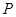到两点
，
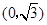的距离之和等于
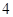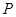，设点的轨迹为
。
（1）求曲线的方程；
（2）过点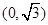
作两条互相垂直的直线
分别与曲线交于
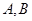和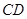
。
①以线段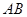
为直径的圆过能否过坐标原点，若能求出此时的
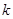值，若不能说明理由；
②求四边形
面积的取值范围。
相关试题
，其中
时，判断函数
在定义域上的单调性；
，不等式
都成立。
的前n项和为
，且
。
是等比数列；
满足
，且
，求数列
。
的最小正周期及在区间
上的最大值和最小值；
，
，求
的值。
，
，其中
，a、b为常数，已知曲线
在点（2,0）处有相同的切线
。
单调区间与极值。
中，
为等腰直角三角形，
，且
，E、F分别为
、BC的中点。
；
的余弦值。推荐套卷
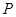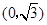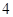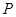在直角坐标系中，点到两点，的距离之和等于，设点的轨迹为。
（1）求曲线的方程；
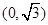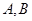（2）过点作两条互相垂直的直线分别与曲线交于和。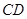
①以线段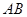为直径的圆过能否过坐标原点，若能求出此时的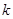值，若不能说明理由；
②求四边形面积的取值范围。
粤公网安备 44130202000953号