正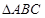
的中线AF与中位线DE相交于G，已知
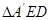是
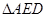绕边DE旋转过程中的一个图形，给出四个命题：
①动点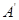
在
上的射影在线段
上；
②恒有
;
③三棱锥
的体积有最大值;
④异面直线
与
不可能垂直．以上正确的命题序号是
，且
，则
．
的定义域为.
，
，且
，则实数
的值是．
______________.
，
.
__________________________.推荐套卷
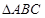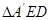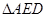正的中线AF与中位线DE相交于G，已知是绕边DE旋转过程中的一个图形，给出四个命题：
①动点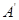在上的射影在线段上；
②恒有;
③三棱锥的体积有最大值;
④异面直线与不可能垂直．以上正确的命题序号是
粤公网安备 44130202000953号