(本小题满分12分)
某公司生产甲、乙两种桶装产品。已知生产甲产品1桶需耗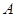 原料1千克、
原料1千克、 原料2千克;生产乙产品1桶需耗
原料2千克;生产乙产品1桶需耗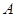 原料2千克,
原料2千克, 原料1千克。每桶甲产品的利润是300元,每桶乙产品的利润是400元。公司在生产这两种产品的计划中,要求每天消耗
原料1千克。每桶甲产品的利润是300元,每桶乙产品的利润是400元。公司在生产这两种产品的计划中,要求每天消耗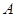 、
、 原料都不能超过12千克。求该公司怎样安排生产计划,可使公司获得最大利润,并求出最大利润.
原料都不能超过12千克。求该公司怎样安排生产计划,可使公司获得最大利润,并求出最大利润.
推荐套卷
(本小题满分12分)
某公司生产甲、乙两种桶装产品。已知生产甲产品1桶需耗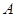 原料1千克、
原料1千克、 原料2千克;生产乙产品1桶需耗
原料2千克;生产乙产品1桶需耗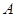 原料2千克,
原料2千克, 原料1千克。每桶甲产品的利润是300元,每桶乙产品的利润是400元。公司在生产这两种产品的计划中,要求每天消耗
原料1千克。每桶甲产品的利润是300元,每桶乙产品的利润是400元。公司在生产这两种产品的计划中,要求每天消耗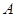 、
、 原料都不能超过12千克。求该公司怎样安排生产计划,可使公司获得最大利润,并求出最大利润.
原料都不能超过12千克。求该公司怎样安排生产计划,可使公司获得最大利润,并求出最大利润.