已知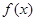 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 且
且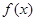 在区间
在区间 上的最大值是12.
上的最大值是12.
(Ⅰ)求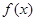 的解析式;
的解析式;
(Ⅱ)是否存在自然数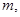 使得方程
使得方程 在区间
在区间 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出 的集合;若不存在,说明理由.
的集合;若不存在,说明理由.
相关知识点
推荐套卷
已知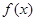 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 且
且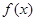 在区间
在区间 上的最大值是12.
上的最大值是12.
(Ⅰ)求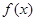 的解析式;
的解析式;
(Ⅱ)是否存在自然数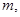 使得方程
使得方程 在区间
在区间 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出 的集合;若不存在,说明理由.
的集合;若不存在,说明理由.