某公司试销一种新产品，规定试销时销售单价不低于成本单价500元/件，又不高于800元/件，经试销调查，发现销售量y（件）与销售单价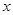
（元/件），可近似看做一次函数
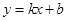的关系（图象如下图所示）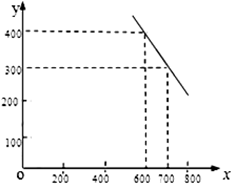
（1）根据图象，求一次函数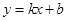的表达式；
（2）设公司获得的毛利润为S元,
①求S关于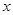的函数表达式；
②求该公司可获得的最大毛利润，并求出此时相应的销售单价．
（提示：毛利润＝销售总价－成本总价）
相关试题
是一次函数，且满足
，求
，求
在闭区间
上的最小值记为
且
，
的值；
在
上的单调性，并用定义证明．
的奇函数
，当
时, 
．
．
，求
．推荐套卷
某公司试销一种新产品，规定试销时销售单价不低于成本单价500元/件，又不高于800元/件，经试销调查，发现销售量y（件）与销售单价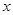（元/件），可近似看做一次函数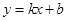的关系（图象如下图所示）
（1）根据图象，求一次函数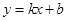的表达式；
（2）设公司获得的毛利润为S元,
①求S关于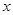的函数表达式；
②求该公司可获得的最大毛利润，并求出此时相应的销售单价．
（提示：毛利润＝销售总价－成本总价）
粤公网安备 44130202000953号