在△ABC中，
分别为内角A.B.C所对的边，且满足
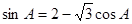
（1）求角A的大小
（2）现给出三个条件：①
②
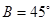③
试从中选出两个可以确定△ABC的条件写出你的选择，并以此为依据求△ABC的面积（只需写出一个选定方案即可，选多种方案以第一种方案记分）
，其中
，且
．求
的最大值和最小值．
、
分别是
的外接圆和内切圆；证明：过
，都可作一个三角形
，使得
的外接圆和内切圆．
的所有排列
的集合为
；
，记
，
；求
．（其中
的元素个数）．
的最小值，使得存在以红点为顶点的
，
；
．推荐套卷
在△ABC中，分别为内角A.B.C所对的边，且满足
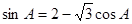
（1）求角A的大小
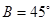（2）现给出三个条件：①②③试从中选出两个可以确定△ABC的条件写出你的选择，并以此为依据求△ABC的面积（只需写出一个选定方案即可，选多种方案以第一种方案记分）
粤公网安备 44130202000953号