已知函数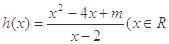 ,且
,且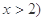 ,函数
,函数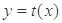 的图象经过点
的图象经过点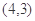 ,且
,且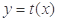 与
与 的图象关于直线
的图象关于直线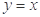 对称,将函数
对称,将函数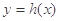 的图象向左平移2个单位后得到函数
的图象向左平移2个单位后得到函数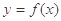 的图象.
的图象.
(Ⅰ)求函数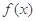 的解析式;
的解析式;
(Ⅱ)若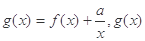 在区间
在区间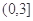 上的值不小于8,求实数
上的值不小于8,求实数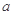 的取值范围.
的取值范围.
(III)若函数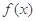 满足:对任意的
满足:对任意的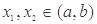 (其中
(其中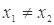 ),有
),有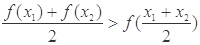 ,称函数
,称函数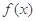 在
在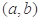 的图象是“下凸的”.判断此题中的函数
的图象是“下凸的”.判断此题中的函数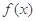 图象在
图象在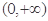 是否是“下凸的”?如果是,给出证明;如果不是,说明理由.
是否是“下凸的”?如果是,给出证明;如果不是,说明理由.
相关知识点
推荐套卷
已知函数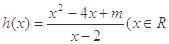 ,且
,且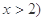 ,函数
,函数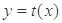 的图象经过点
的图象经过点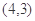 ,且
,且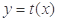 与
与 的图象关于直线
的图象关于直线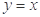 对称,将函数
对称,将函数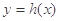 的图象向左平移2个单位后得到函数
的图象向左平移2个单位后得到函数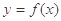 的图象.
的图象.
(Ⅰ)求函数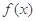 的解析式;
的解析式;
(Ⅱ)若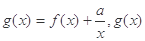 在区间
在区间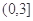 上的值不小于8,求实数
上的值不小于8,求实数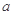 的取值范围.
的取值范围.
(III)若函数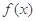 满足:对任意的
满足:对任意的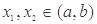 (其中
(其中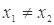 ),有
),有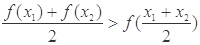 ,称函数
,称函数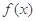 在
在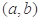 的图象是“下凸的”.判断此题中的函数
的图象是“下凸的”.判断此题中的函数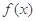 图象在
图象在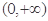 是否是“下凸的”?如果是,给出证明;如果不是,说明理由.
是否是“下凸的”?如果是,给出证明;如果不是,说明理由.