设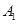
，
，
，
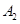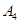是平面直角坐标系中两两不同的四点，若
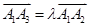(λ∈R)，
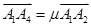(μ∈R)，且
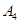,则称，调和分割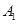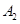， ,已知点C(c，o),D(d，O) (c，d∈R)调和分割点A(0，0)，B(1，0)，则下面说法正确的是( )
| A．C可能是线段AB的中点 | B．D可能是线段AB的中点 |
| C．C，D可能同时在线段AB上 | D．C，D不可能同时在线段AB的延长线上 |
相关试题
，则动点P的轨迹方程是（ ）
推荐套卷
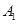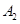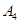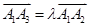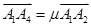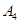设，，，是平面直角坐标系中两两不同的四点，若 (λ∈R)，(μ∈R)，且,则称，调和分割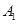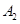， ,已知点C(c，o),D(d，O) (c，d∈R)调和分割点A(0，0)，B(1，0)，则下面说法正确的是( )
| A．C可能是线段AB的中点 | B．D可能是线段AB的中点 |
| C．C，D可能同时在线段AB上 | D．C，D不可能同时在线段AB的延长线上 |
粤公网安备 44130202000953号