平面向量也叫二维向量,二维向量的坐标表示及其运算可以推广到n(n≥3)维向量,n维向量可用(x1,x2,x3,x4,…,xn)表示.设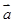 =(a1,a2,a3,a4,…,an),
=(a1,a2,a3,a4,…,an), =(b1,b2,b3,b4,…,bn),规定向量
=(b1,b2,b3,b4,…,bn),规定向量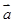 与
与 夹角θ的余弦为cosθ=
夹角θ的余弦为cosθ= .已知n维向量
.已知n维向量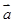 ,
, ,当
,当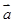 =(1,1,1,1,…,1),
=(1,1,1,1,…,1), =(-1,-1,1,1,1,…,1)时,cosθ等于______________
=(-1,-1,1,1,1,…,1)时,cosθ等于______________
推荐套卷
平面向量也叫二维向量,二维向量的坐标表示及其运算可以推广到n(n≥3)维向量,n维向量可用(x1,x2,x3,x4,…,xn)表示.设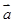 =(a1,a2,a3,a4,…,an),
=(a1,a2,a3,a4,…,an), =(b1,b2,b3,b4,…,bn),规定向量
=(b1,b2,b3,b4,…,bn),规定向量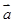 与
与 夹角θ的余弦为cosθ=
夹角θ的余弦为cosθ= .已知n维向量
.已知n维向量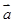 ,
, ,当
,当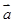 =(1,1,1,1,…,1),
=(1,1,1,1,…,1), =(-1,-1,1,1,1,…,1)时,cosθ等于______________
=(-1,-1,1,1,1,…,1)时,cosθ等于______________