、设函数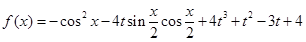
，
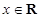，其中|t|≤1，将f(x)的最小值记为g(t)．
(1)求g(t)的表达式；
(2)对于区间[－1，1]中的某个t，是否存在实数a，使得不等式g(t)≤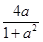
成立？如果存在，求出这样的a及其对应的t；如果不存在，请说明理由．
是减函数，求
的取值范围
上的函数
，若关于
的
，有3个不同实数解
，且
，则下列说法中正确的是：（）
，若对于任意的
，
,且
，求证：存在
使得
>0时，
=
>
恒成立，求正整数
的最大值
是定义在
上的单调递增函数，对于任意的
满足
，且
满足
推荐套卷
、设函数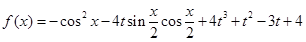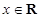，，其中|t|≤1，将f(x)的最小值记为g(t)．
(1)求g(t)的表达式；
(2)对于区间[－1，1]中的某个t，是否存在实数a，使得不等式g(t)≤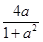成立？如果存在，求出这样的a及其对应的t；如果不存在，请说明理由．
粤公网安备 44130202000953号