如图,在直角坐标系中,O为坐标原点,直线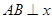 轴于点
轴于点 ,
, 动点
动点 到直线
到直线 的距离是它到点
的距离是它到点 的距离的2倍.
的距离的2倍.
(I)求点 的轨迹方程;
的轨迹方程;
(II)设点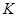 为点
为点 的轨迹与
的轨迹与 轴正半轴的交点,直线
轴正半轴的交点,直线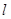 交点
交点 的轨迹于
的轨迹于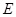 ,
,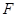 两点(
两点(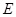 ,
,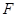 与点
与点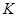 不重合),且满足
不重合),且满足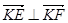 ,动点
,动点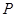 满足
满足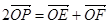 ,求直线
,求直线 的斜率的取值范围.
的斜率的取值范围.
推荐套卷
如图,在直角坐标系中,O为坐标原点,直线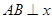 轴于点
轴于点 ,
, 动点
动点 到直线
到直线 的距离是它到点
的距离是它到点 的距离的2倍.
的距离的2倍.
(I)求点 的轨迹方程;
的轨迹方程;
(II)设点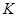 为点
为点 的轨迹与
的轨迹与 轴正半轴的交点,直线
轴正半轴的交点,直线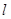 交点
交点 的轨迹于
的轨迹于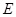 ,
,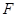 两点(
两点(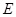 ,
,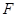 与点
与点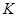 不重合),且满足
不重合),且满足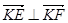 ,动点
,动点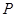 满足
满足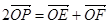 ,求直线
,求直线 的斜率的取值范围.
的斜率的取值范围.