为美化环境,某地决定在一个大型广场建一个同心圆形花坛,花坛分为两部分,中间小圆部分种植草坪,周围的圆环分为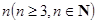 等份种植红、黄、蓝三色不同的花. 要求相邻两部分种植不同颜色的花. 如图①,圆环分成的
等份种植红、黄、蓝三色不同的花. 要求相邻两部分种植不同颜色的花. 如图①,圆环分成的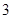 等份分别为
等份分别为 ,
,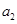 ,
,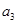 ,有
,有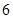 种不同的种植方法.
种不同的种植方法.
(1)如图②,圆环分成的4等份分别为 ,
,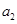 ,
,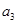 ,
, ,有 种不同的种植方法;
,有 种不同的种植方法;
(2)如图③,圆环分成的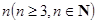 等份分别为
等份分别为 ,
,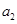 ,
,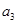 ,
,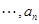 , 有 种不同的种植方法.
, 有 种不同的种植方法.
推荐套卷
为美化环境,某地决定在一个大型广场建一个同心圆形花坛,花坛分为两部分,中间小圆部分种植草坪,周围的圆环分为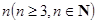 等份种植红、黄、蓝三色不同的花. 要求相邻两部分种植不同颜色的花. 如图①,圆环分成的
等份种植红、黄、蓝三色不同的花. 要求相邻两部分种植不同颜色的花. 如图①,圆环分成的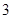 等份分别为
等份分别为 ,
,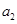 ,
,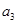 ,有
,有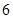 种不同的种植方法.
种不同的种植方法.
(1)如图②,圆环分成的4等份分别为 ,
,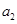 ,
,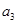 ,
, ,有 种不同的种植方法;
,有 种不同的种植方法;
(2)如图③,圆环分成的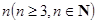 等份分别为
等份分别为 ,
,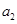 ,
,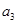 ,
,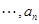 , 有 种不同的种植方法.
, 有 种不同的种植方法.