深圳市某校中学生篮球队假期集训，集训前共有6个篮球，其中3个是新球（即没有用过的球），3个是旧球（即至少用过一次的球）．每次训练，都从中任意取出2个球，用完后放回．
（1）设第一次训练时取到的新球个数为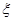
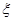，求的分布列和数学期望；
（2）求第二次训练时恰好取到一个新球的概率．
相关试题
，其中
在区间
上的值域
中，
,
,
分别是角
的对边,
，且
,
，求边
：实数
满足
，其中
；命题
：实数
，且
是
的充分不必要条件，求实数
的取值范围．
．
，若
，且△ABC是锐角三角形，求
的取值范围．
的值；（2）写出函数在
上的单调区间和值域。
,
，解不等式
；
有最小值，求实数
的取值范围.推荐套卷
深圳市某校中学生篮球队假期集训，集训前共有6个篮球，其中3个是新球（即没有用过的球），3个是旧球（即至少用过一次的球）．每次训练，都从中任意取出2个球，用完后放回．
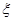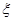（1）设第一次训练时取到的新球个数为，求的分布列和数学期望；
（2）求第二次训练时恰好取到一个新球的概率．
粤公网安备 44130202000953号