已知函数
在[1，＋∞）上为增函数，且
，
，
∈R．
（1）求θ的值；
（2）若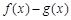
在[1，＋∞）上为单调函数，求m的取值范围；
（3）设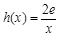
，若在[1，e]上至少存在一个
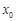，使得
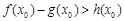成立，
求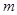
的取值范围．
相关试题
相关知识点
推荐套卷
已知函数在[1，＋∞）上为增函数，且，，∈R．
（1）求θ的值；
（2）若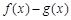在[1，＋∞）上为单调函数，求m的取值范围；
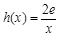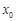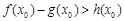（3）设，若在[1，e]上至少存在一个，使得成立，
求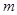的取值范围．
粤公网安备 44130202000953号