如图所示, 是定义在区间
是定义在区间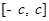 (
( )上的奇函数,令
)上的奇函数,令 ,并有关于函数
,并有关于函数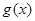 的四个论断:
的四个论断: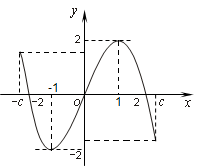
①若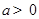 ,对于
,对于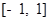 内的任意实数
内的任意实数 (
(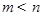 ),
),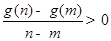 恒成立;
恒成立;
②函数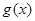 是奇函数的充要条件是
是奇函数的充要条件是 ;
;
③若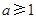 ,
, ,则方程
,则方程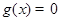 必有3个实数根;
必有3个实数根;
④ ,
,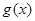 的导函数
的导函数
 有两个零点;
有两个零点;
其中所有正确结论的序号是**_.
推荐套卷
如图所示, 是定义在区间
是定义在区间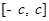 (
( )上的奇函数,令
)上的奇函数,令 ,并有关于函数
,并有关于函数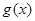 的四个论断:
的四个论断:
①若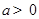 ,对于
,对于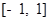 内的任意实数
内的任意实数 (
(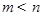 ),
),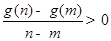 恒成立;
恒成立;
②函数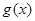 是奇函数的充要条件是
是奇函数的充要条件是 ;
;
③若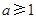 ,
, ,则方程
,则方程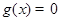 必有3个实数根;
必有3个实数根;
④ ,
,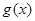 的导函数
的导函数
 有两个零点;
有两个零点;
其中所有正确结论的序号是**_.