(本小题满分15分)
已知函数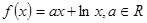
(Ⅰ)求函数 的极值;
的极值;
(Ⅱ)对于曲线上的不同两点 ,如果存在曲线上的点
,如果存在曲线上的点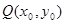 ,且
,且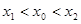 ,使得曲线在点
,使得曲线在点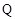 处的切线
处的切线 ∥
∥ ,则称
,则称 为弦
为弦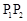 的伴随切线。特别地,当
的伴随切线。特别地,当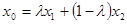 ,
,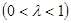 时,又称
时,又称 为
为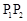 的λ——伴随切线。
的λ——伴随切线。
(ⅰ)求证:曲线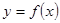 的任意一条弦均有伴随切线,并且伴随切线是唯一的;
的任意一条弦均有伴随切线,并且伴随切线是唯一的;
(ⅱ)是否存在曲线C,使得曲线C的任意一条弦均有 伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。
伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。
相关知识点
推荐套卷
(本小题满分15分)
已知函数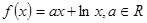
(Ⅰ)求函数 的极值;
的极值;
(Ⅱ)对于曲线上的不同两点 ,如果存在曲线上的点
,如果存在曲线上的点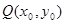 ,且
,且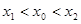 ,使得曲线在点
,使得曲线在点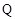 处的切线
处的切线 ∥
∥ ,则称
,则称 为弦
为弦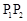 的伴随切线。特别地,当
的伴随切线。特别地,当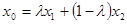 ,
,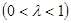 时,又称
时,又称 为
为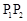 的λ——伴随切线。
的λ——伴随切线。
(ⅰ)求证:曲线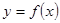 的任意一条弦均有伴随切线,并且伴随切线是唯一的;
的任意一条弦均有伴随切线,并且伴随切线是唯一的;
(ⅱ)是否存在曲线C,使得曲线C的任意一条弦均有 伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。
伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。