在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则AB2+AC2=BC2”拓展到空间，类比平面几何的勾股定理，“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂直，则可得”猜想正确的是（ ）
A．AB2+AC2+ AD2=BC2 +CD2 +BD2 B．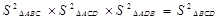
C．
D．AB2×AC2×AD2=BC2×CD2×BD2
相关试题
，
，设
是△
内的一点(不在边界上)，定义
，其中
分别表示△
,△
,△
的面积，若
，则
的最大值为（）
，则
的值为（）
中，内角
的对边分别为
，若
，则
的取值范围是（）
，
是
上的一点，若
，
的值为（）
，则
的取值范围为（ ）
推荐套卷
在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则AB2+AC2=BC2”拓展到空间，类比平面几何的勾股定理，“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂直，则可得”猜想正确的是（ ）
A．AB2+AC2+ AD2=BC2 +CD2 +BD2 B．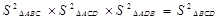
C． D．AB2×AC2×AD2=BC2×CD2×BD2
粤公网安备 44130202000953号