在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,记为[k],即[k]={5n+k|n∈Z},k=0,1,2,3,4.给出如下四个结论:
① 2011∈[1];
② -3 ∈ [3];
③ z="[0]∪[1]" ∪[2] ∪[3] ∪[4];
④“整数a,b属于同一‘类”的充要条件是“a-b∈[0]”
其中,正确结论的个数是
| A.1 | B.2 | C.3 | D.4 |
相关知识点
推荐套卷
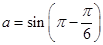 ,函数
,函数 ,则
,则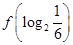 的值等于()
的值等于()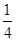
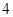

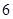
 ,向量
,向量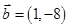 ,若
,若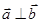 ,则实数
,则实数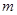 的值是()
的值是()
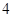

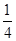
 ,集合
,集合 ,则
,则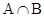 等于()
等于()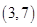
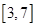

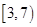
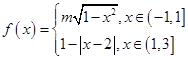 ,其中
,其中 ,且函数
,且函数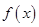 满足
满足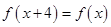 .若方程
.若方程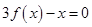 恰有
恰有 个根,则实数
个根,则实数 的取值范围是()
的取值范围是()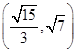
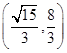

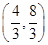
 为原点,双曲线
为原点,双曲线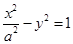 (
(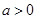 )上有一点
)上有一点 ,过
,过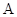 ,
,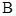 ,平行四边形
,平行四边形 的面积为
的面积为 ,则双曲线的离心率为()
,则双曲线的离心率为()
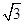
 粤公网安备 44130202000953号
粤公网安备 44130202000953号