已知a与b均为单位向量，其夹角为θ，有下列四个命题：
p1：|a＋b|＞1⇔θ∈
； p2：|a＋b|＞1⇔θ∈
p3：|a－b|＞1⇔θ∈
； p4：|a－b|＞1⇔θ∈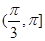
.
其中的真命题是( )
| A．p1，p4 | B．p1，p3 | C．p2，p3 | D．p2，p4 |
相关试题
是等比数列，且
的公比
为（
）
等于（）
，其中
是虚数单位，则复数
的实部与虚部
之和为（）
上的值域为[-1,3]，则点
的轨迹是图中的（）
的映射
的个数是（）相关知识点
推荐套卷
已知a与b均为单位向量，其夹角为θ，有下列四个命题：
p1：|a＋b|＞1⇔θ∈； p2：|a＋b|＞1⇔θ∈
p3：|a－b|＞1⇔θ∈； p4：|a－b|＞1⇔θ∈.
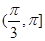其中的真命题是( )
| A．p1，p4 | B．p1，p3 | C．p2，p3 | D．p2，p4 |
粤公网安备 44130202000953号