已知数列{an}各项均为正数,Sn为其前n项和,对于 ,总有
,总有 成等差数列.
成等差数列.
(I )求数列{an}的通项an;
(II)设数列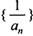 的前n项和为Tn,数列{Tn}的前n项和为Rn,求证:
的前n项和为Tn,数列{Tn}的前n项和为Rn,求证: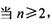
 时,
时, ;
;
(III)对任意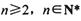 ,试比较
,试比较 与
与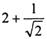 的大小
的大小
推荐套卷
已知数列{an}各项均为正数,Sn为其前n项和,对于 ,总有
,总有 成等差数列.
成等差数列.
(I )求数列{an}的通项an;
(II)设数列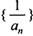 的前n项和为Tn,数列{Tn}的前n项和为Rn,求证:
的前n项和为Tn,数列{Tn}的前n项和为Rn,求证: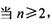
 时,
时, ;
;
(III)对任意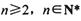 ,试比较
,试比较 与
与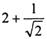 的大小
的大小