为了求函数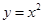 ,函数
,函数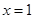 ,
,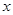 轴围成的曲边三角形的面积
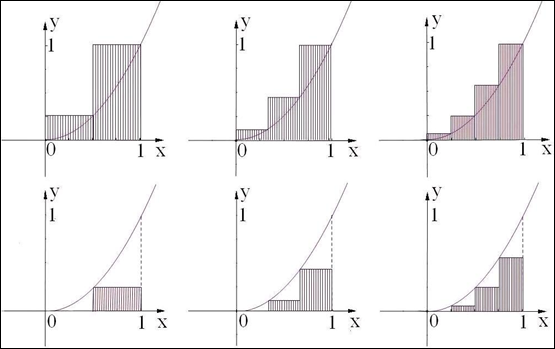
轴围成的曲边三角形的面积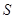 ,古人想出了两种方案求其近似解(如图):第一次将区间
,古人想出了两种方案求其近似解(如图):第一次将区间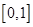 二等分,求出阴影部分矩形面积,记为
二等分,求出阴影部分矩形面积,记为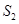 ;第二次将区间
;第二次将区间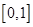 三等分,求出阴影部分矩形面积,记为
三等分,求出阴影部分矩形面积,记为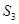 ;第三次将区间
;第三次将区间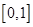 四等分,求出
四等分,求出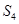
……依此类推,记方案一中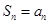 ,方案二中
,方案二中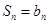 ,其中
,其中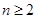
1. 求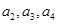
2. 求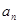 的通项公式,并证明
的通项公式,并证明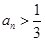
3. 求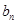 的通项公式,类比第②步,猜想
的通项公式,类比第②步,猜想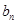 的取值范围。并由此推出
的取值范围。并由此推出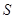 的值(只需直接写出
的值(只需直接写出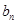 的范围与
的范围与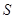 的值,无须证明)
的值,无须证明)
参考公式: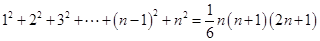
相关知识点
推荐套卷
 的各项都是正数,且对任意
的各项都是正数,且对任意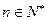 ,都有
,都有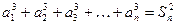 ,记
,记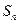 为数列
为数列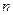 项和.(Ⅰ)求数列
项和.(Ⅰ)求数列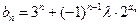 (
( 为非零常数,
为非零常数,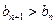 .
.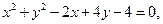 是否存在斜率为1的直线
是否存在斜率为1的直线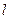 ,使
,使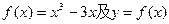 上一点P(1,-2),过点P作直线l,(Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程;(Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);(Ⅲ)在(Ⅱ)的条件下,求
上一点P(1,-2),过点P作直线l,(Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程;(Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);(Ⅲ)在(Ⅱ)的条件下,求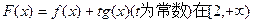 上单调时,t的取值范围.
上单调时,t的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号