已知三条不重合的直线m,n,l，两个不重合的平面α，β有下列命题：
①若m∥n,n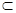
α，则m∥α ②若l⊥α，m⊥β，且l∥m,则α∥β
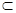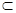③若mα，nα,m∥β，n∥β，则α∥β ④若α⊥β，α
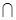β＝m, n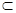β,n⊥m,则n⊥α；
其中正确命题的个数是（ ）
| A．1 | B．2 | C．3 | D．4 |
，则z＝2x＋y的最大值等于( )
的图象大致是( )
，则
的值为( )
”是“
”的( )
的解
属于区间 ( )
相关知识点
推荐套卷
已知三条不重合的直线m,n,l，两个不重合的平面α，β有下列命题：
①若m∥n,n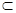α，则m∥α ②若l⊥α，m⊥β，且l∥m,则α∥β
③若m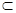α，n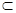α,m∥β，n∥β，则α∥β ④若α⊥β，α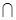β＝m, n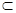β,n⊥m,则n⊥α；
其中正确命题的个数是（ ）
| A．1 | B．2 | C．3 | D．4 |
粤公网安备 44130202000953号