设平面内两定点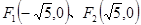
，直线PF1和PF2相交于点P,且它们的斜率之积为定值
；
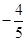（Ⅰ）求动点P的轨迹C1的方程；
（Ⅱ）设M（0，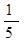
），N为抛物线C2：
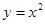上的一动点，过点N作抛物线C2的切线交曲线C1于P、Q两点，求
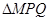面积的最大值．
相关试题
是夹角为
的单位向量，且
，
．
；
与
的夹角
．
在
上无零点，请你探究函数
在
，若对任意的
，恒有
成立，求实数
的取值范围．
满足
，则称
为
的不动点．
没有不动点，求实数
的取值范围；
的不动点
，求
的值；
有不动点，求实数
中，底面
是边长为
的菱形，
，
面
，
，
分别为
，
的中点．
面
；
的大小的正弦值；
到面
中，角
所对的边为
．已知
，且
．
的值；
时，求
．推荐套卷
设平面内两定点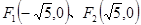，直线PF1和PF2相交于点P,且它们的斜率之积为定值；
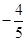（Ⅰ）求动点P的轨迹C1的方程；
（Ⅱ）设M（0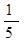，），N为抛物线C2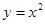：上的一动点，过点N作抛物线C2的切线交曲线C1于P、Q两点，求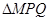面积的最大值．
粤公网安备 44130202000953号