(本小题满分14分)
从椭圆 +
+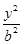 =1(a>b>0)上一点M向x轴作垂线,恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴端点B的连线AB平行于OM.
=1(a>b>0)上一点M向x轴作垂线,恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴端点B的连线AB平行于OM.
(Ⅰ)求椭圆的离心率 ;
(Ⅱ)若b=2,设Q是椭圆上任意一点,F2是右焦点,求△F1QF2的面积的最大值;
(Ⅲ)当QF2^AB时,延长QF2与椭圆交于另一点P,若DF1PQ的面积为20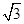 (Q是椭圆上的点),求此椭圆的方程。
(Q是椭圆上的点),求此椭圆的方程。
推荐套卷
(本小题满分14分)
从椭圆 +
+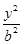 =1(a>b>0)上一点M向x轴作垂线,恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴端点B的连线AB平行于OM.
=1(a>b>0)上一点M向x轴作垂线,恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴端点B的连线AB平行于OM.
(Ⅰ)求椭圆的离心率 ;
(Ⅱ)若b=2,设Q是椭圆上任意一点,F2是右焦点,求△F1QF2的面积的最大值;
(Ⅲ)当QF2^AB时,延长QF2与椭圆交于另一点P,若DF1PQ的面积为20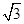 (Q是椭圆上的点),求此椭圆的方程。
(Q是椭圆上的点),求此椭圆的方程。