观察下列等式：
1=1 13=1
1+2=3 13+23=9
1+2+3=6 13+23+33=36
1+2+3+4=10 13+23+33+43=100
1+2+3+4+5=15 13+23+33+43+53=225
……
可以推测：13+23+33+…+n3= 。（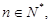
用含有n的代数式表示）
的定义域为R，则a的取值范围为_。
，
恒成立，则
的取值范围是.
满足：对任意的
，有
成立，则推荐套卷
观察下列等式：
1=1 13=1
1+2=3 13+23=9
1+2+3=6 13+23+33=36
1+2+3+4=10 13+23+33+43=100
1+2+3+4+5=15 13+23+33+43+53=225
……
可以推测：13+23+33+…+n3= 。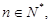（用含有n的代数式表示）
粤公网安备 44130202000953号