某同学准备用反证法证明如下问题:函数f(x)在[0,1]上有意义,且f(0)=f(1),如果对于不同的x1,x2∈[0,1]都有|f(x1)-f(x2)|<|x1-x2|,求证:|f(x1)-f(x2)|<,那么它的假设应该是( ).
| A.“对于不同的x1,x2∈[0,1],都得|f(x1)-f(x2)|<|x1-x2| 则|f(x1)-f(x2)|≥” |
| B.“对于不同的x1,x2∈[0,1],都得|f(x1)-f(x2)|> |x1-x2| 则|f(x1)-f(x2)|≥” |
| C.“∃x1,x2∈[0,1],使得当|f(x1)-f(x2)|<|x1-x2| 时有|f(x1)-f(x2)|≥” |
| D.“∃x1,x2∈[0,1],使得当|f(x1)-f(x2)|>|x1-x2|时有|f(x1)-f(x2)|≥” |
相关知识点
推荐套卷
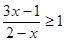 的解集是()
的解集是()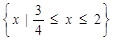
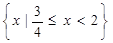
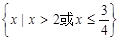

 ,则
,则
 ,则
,则 ,则
,则
 ,则
,则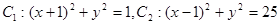 ,动圆
,动圆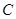 与圆
与圆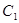 外切,与圆
外切,与圆 内切,则圆
内切,则圆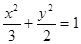
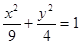

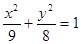
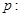 双曲线
双曲线 上一点
上一点 到左焦点距离为
到左焦点距离为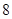 ,则
,则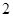 或
或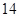 ;命题
;命题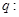 椭圆离心率越大,椭圆越趋近于圆. 则下列命题中为真命题的是
椭圆离心率越大,椭圆越趋近于圆. 则下列命题中为真命题的是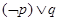
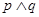

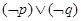
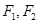 是双曲线
是双曲线 的两焦点,以点
的两焦点,以点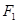 为直角顶点作等腰直角三角形
为直角顶点作等腰直角三角形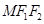 ,若边
,若边 的中点在双曲线上,则双曲线的离心率是
的中点在双曲线上,则双曲线的离心率是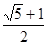
 粤公网安备 44130202000953号
粤公网安备 44130202000953号