已知数列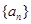 的前
的前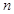 项和为
项和为
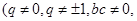
 ,现把数列
,现把数列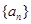 的各项排成如图所示的三角形形状.记
的各项排成如图所示的三角形形状.记 为第
为第 行从左起第
行从左起第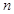 个数
个数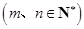 .
.
有下列命题:
①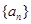 为等比数列且其公比
为等比数列且其公比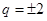 ;
;
②当 时
时 不存在;
不存在;
③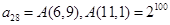 ;
;
④假设 为大于
为大于 的常数,且
的常数,且 ,
,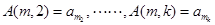 ,其中
,其中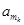 为
为 的最大值,从所有
的最大值,从所有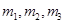 ,
, 
 中任取一个数,若取得的数恰好为奇数的概率为
中任取一个数,若取得的数恰好为奇数的概率为 ,则
,则 必然为偶数.
必然为偶数.
其中你认为正确的所有命题的序号是___________.
相关知识点
推荐套卷
已知数列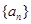 的前
的前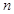 项和为
项和为
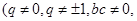
 ,现把数列
,现把数列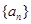 的各项排成如图所示的三角形形状.记
的各项排成如图所示的三角形形状.记 为第
为第 行从左起第
行从左起第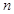 个数
个数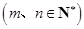 .
.
有下列命题:
①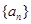 为等比数列且其公比
为等比数列且其公比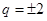 ;
;
②当 时
时 不存在;
不存在;
③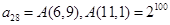 ;
;
④假设 为大于
为大于 的常数,且
的常数,且 ,
,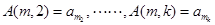 ,其中
,其中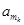 为
为 的最大值,从所有
的最大值,从所有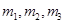 ,
, 
 中任取一个数,若取得的数恰好为奇数的概率为
中任取一个数,若取得的数恰好为奇数的概率为 ,则
,则 必然为偶数.
必然为偶数.
其中你认为正确的所有命题的序号是___________.