已知二次函数 直线
直线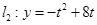 (其中
(其中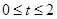 ,
,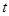 为常数);
为常数); .若直线
.若直线 1、
1、 2与函数
2与函数 的图象以及
的图象以及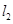 ,
, 轴与函数
轴与函数 的图象所围成的封闭图形如阴影所示.
的图象所围成的封闭图形如阴影所示.
(1)求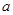 、
、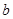 、
、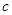 的值;
的值;
(2)求阴影面积 关于
关于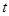 的函数
的函数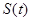 的解析式;
的解析式;
(3)若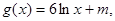 问是否存在实数
问是否存在实数 ,使得
,使得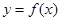 的图象与
的图象与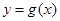 的图象有且只有两个不同的交点?若存在,求出
的图象有且只有两个不同的交点?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
推荐套卷
已知二次函数 直线
直线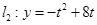 (其中
(其中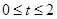 ,
,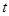 为常数);
为常数); .若直线
.若直线 1、
1、 2与函数
2与函数 的图象以及
的图象以及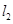 ,
, 轴与函数
轴与函数 的图象所围成的封闭图形如阴影所示.
的图象所围成的封闭图形如阴影所示.
(1)求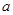 、
、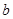 、
、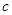 的值;
的值;
(2)求阴影面积 关于
关于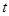 的函数
的函数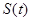 的解析式;
的解析式;
(3)若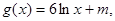 问是否存在实数
问是否存在实数 ,使得
,使得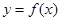 的图象与
的图象与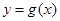 的图象有且只有两个不同的交点?若存在,求出
的图象有且只有两个不同的交点?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.