下面给出了关于复数的四种类比推理:
① 复数的加减法运算法则,可以类比多项式的加减法运算法则;
② 由向量 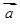 的性质
的性质  ,可以类比得到复数
,可以类比得到复数 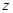 的性质
的性质 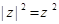 ;
;
③ 方程 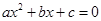 (a 、b 、c ∈ R )有两个不同实根的条件是
(a 、b 、c ∈ R )有两个不同实根的条件是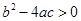 , 类比可以得到 方程
, 类比可以得到 方程  (a 、b 、c ∈ C)有两个不同复数根的条件是
(a 、b 、c ∈ C)有两个不同复数根的条件是 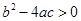 ;
;
④ 由向量加法的几何意义,可以类比得到复数加法的几何意义.
其中类比得到的结论正确的是( )
A、① ③ B、 ② ④ C、② ③ D、① ④
推荐套卷
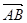 与
与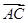 的夹角为
的夹角为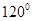 ,且
,且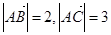 ,若
,若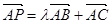 ,且,
,且,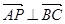 ,则实数
,则实数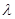 的值为()
的值为()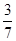
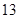
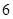
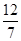
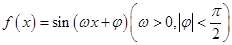 的最小正周期是
的最小正周期是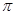 ,若其图象向右平移
,若其图象向右平移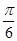 个单位后得到的函数为奇函数,则函数
个单位后得到的函数为奇函数,则函数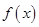 的图象( )
的图象( )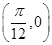 对称
对称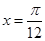 对称
对称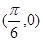 对称
对称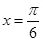 对称
对称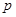 为假命题,命题
为假命题,命题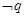 为假命题,则命题“
为假命题,则命题“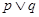 ”为假命题;
”为假命题;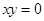 ,则
,则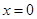 或
或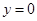 ”的否命题为“若
”的否命题为“若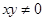 ,则
,则 或
或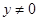 ”;
”;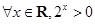 ”的否定是“
”的否定是“ 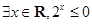 ”.则以上结论正确的个数为( )
”.则以上结论正确的个数为( )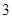
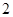
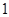

 则函数
则函数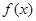 的零点为( )
的零点为( )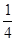 和1
和1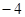 和0
和0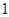
 是等差数列,若
是等差数列,若 则数列
则数列 粤公网安备 44130202000953号
粤公网安备 44130202000953号