某种游戏中,黑、黄两个“电子狗”从棱和为1的正方体ABCD-A1B1C1D1的顶点A出发沿棱
向前爬行,每爬完一条棱称为“爬完一段”,黑“电子狗”爬行的路线是AA1→A1D1→…,黄
“电子狗”爬行的路线是AB→BB1→…,它们都遵循如下规则:所爬行的第i+2段与第i段
所在直线必须异面直线(其中i是正整数).设黑“电子狗”爬完2012段、黄“电子狗”爬完
2011段后各自停止在正方体的某个顶点处,这时黑、黄“电子狗”间的距离是( )
| A. 0 | B. 1 | C.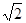 |
D.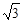 |
推荐套卷
某种游戏中,黑、黄两个“电子狗”从棱和为1的正方体ABCD-A1B1C1D1的顶点A出发沿棱
向前爬行,每爬完一条棱称为“爬完一段”,黑“电子狗”爬行的路线是AA1→A1D1→…,黄
“电子狗”爬行的路线是AB→BB1→…,它们都遵循如下规则:所爬行的第i+2段与第i段
所在直线必须异面直线(其中i是正整数).设黑“电子狗”爬完2012段、黄“电子狗”爬完
2011段后各自停止在正方体的某个顶点处,这时黑、黄“电子狗”间的距离是( )
| A. 0 | B. 1 | C.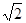 |
D.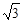 |