(本题满分7分)
已知直线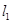 :
: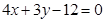 与
与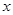 轴和
轴和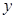 轴分别交于
轴分别交于 两点,直线
两点,直线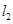 经过点
经过点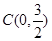 且与直线
且与直线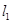 垂直,垂足为
垂直,垂足为 .
.
(Ⅰ)求直线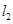 的方程与点
的方程与点 的坐标;
的坐标;
(Ⅱ)若将四边形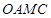 (
(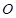 为坐标原点)绕
为坐标原点)绕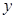 轴旋转一周得到一几何体,求该几何体的体积
轴旋转一周得到一几何体,求该几何体的体积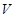 .
.
推荐套卷
(本题满分7分)
已知直线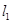 :
: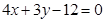 与
与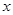 轴和
轴和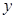 轴分别交于
轴分别交于 两点,直线
两点,直线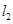 经过点
经过点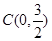 且与直线
且与直线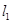 垂直,垂足为
垂直,垂足为 .
.
(Ⅰ)求直线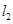 的方程与点
的方程与点 的坐标;
的坐标;
(Ⅱ)若将四边形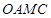 (
(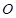 为坐标原点)绕
为坐标原点)绕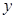 轴旋转一周得到一几何体,求该几何体的体积
轴旋转一周得到一几何体,求该几何体的体积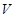 .
.