如图为一建筑物的正视图，尺寸图中标出，为了做好火灾的防备工作，需要在地面上确定安装喷水枪的地点
，经测试只有当
（图中的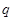
角）时，才能使得水枪喷射能够覆盖整个建筑物，求水枪安装点到建筑物的距离
长．（注：图中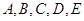
在同一个平面内；不考虑喷水枪的高度．）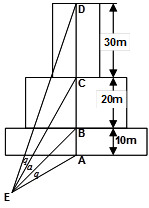
(n>1，n∈N*)的过程中，用n＝k＋1时左边的代数式减去n＝k时左边的代数式的结果是A，求代数式A.
＋
，N＝
＋
，求M与N的大小关系．
，求证：a＞b.
＋
＋
的最大值．
与
的大小．推荐套卷
如图为一建筑物的正视图，尺寸图中标出，为了做好火灾的防备工作，需要在地面上确定安装喷水枪的地点，经测试只有当（图中的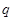角）时，才能使得水枪喷射能够覆盖整个建筑物，求水枪安装点到建筑物的距离长．（注：图中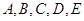在同一个平面内；不考虑喷水枪的高度．）
粤公网安备 44130202000953号