如图，在直三棱柱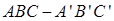
中，
，
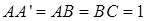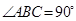．棱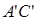
上有两个动点E，F，且EF =" a" （a为常数）．
（Ⅰ）在平面ABC内确定一条直线，使该直线与直线CE垂直；
（Ⅱ）判断三棱锥B—CEF的体积是否为定值．若是定值，求出这个三棱锥的体积；若不是定值，说明理由．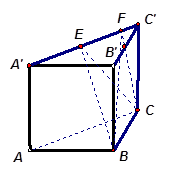
相关试题
的展开式中，奇数项的二项式系数的和等于偶数项的二项式系数的和.
．
的定义域；
，当
时，恒有
．
为正实数，
，并且
，试求
有最小正周期2，且当
时，
．
和
的值；
．
，比较
与
的大小；
时，有
，求实数
的取值范围．相关知识点
推荐套卷
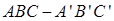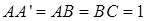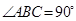如图，在直三棱柱中，，．棱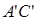上有两个动点E，F，且EF =" a" （a为常数）．
（Ⅰ）在平面ABC内确定一条直线，使该直线与直线CE垂直；
（Ⅱ）判断三棱锥B—CEF的体积是否为定值．若是定值，求出这个三棱锥的体积；若不是定值，说明理由．
粤公网安备 44130202000953号