已知函数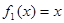
，
，
，
，
，
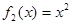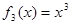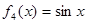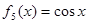，将它们分别写在六张卡片上，放在一个盒子中，
（Ⅰ）现从盒子中任取两张卡片，将卡片上的函数相加得到一个新函数，求所得的
函数是奇函数的概率；
（Ⅱ）从盒子中任取两张卡片，求其中至少一张上为奇函数的概率
相关试题
的解析式；
在
上
时，求f(x)的最大值与最小值；
上是单调函数，且
，求θ的取值范围。
且以
为最小正周期。
，求sinα的值。
与
，
与
；
时，
与
有什么关系？并证明你的发现；
.
的定义域为A，函数
的值域为B。
，且
，求实数a的取值范围。推荐套卷
已知函数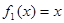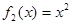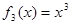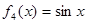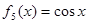，，，，，，将它们分别写在六张卡片上，放在一个盒子中，
（Ⅰ）现从盒子中任取两张卡片，将卡片上的函数相加得到一个新函数，求所得的
函数是奇函数的概率；
（Ⅱ）从盒子中任取两张卡片，求其中至少一张上为奇函数的概率
粤公网安备 44130202000953号