(本题满分16分)本题共有2个小题,第1小题满分6分,第2小题满分10分.
已知两点 、
、 ,点
,点 是直角坐标平面上的动点,若将点
是直角坐标平面上的动点,若将点 的横坐标保持不变、纵坐标扩大到
的横坐标保持不变、纵坐标扩大到 倍后得到点
倍后得到点 满足
满足 .
.
(1) 求动点 所在曲线
所在曲线 的轨迹方程;
的轨迹方程;
(2)(理科)过点 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 于
于 两点,且满足
两点,且满足 ,又点
,又点 关于原点O的对称点为点
关于原点O的对称点为点 ,试问四点
,试问四点 是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
(文科)过点 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 于
于 两点,且满足
两点,且满足 (O为坐标原点),试判断点
(O为坐标原点),试判断点 是否在曲线
是否在曲线 上,并说明理由.
上,并说明理由.
相关知识点
推荐套卷
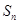 为等差数列
为等差数列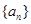 的前
的前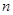 项和,且
项和,且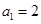 ,
,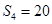 .
.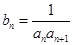 ,求数列
,求数列 的前
的前 为菱形,且
为菱形,且 ,
, .
.
 ;
; ,求二面角
,求二面角 的余弦值。
的余弦值。
 ,求△ABC的面积。
,求△ABC的面积。 为公差不为0的等差数列
为公差不为0的等差数列 的前
的前 项和,且
项和,且 ,
, 成等比数列.
成等比数列. ,求数列
,求数列 的前
的前 在x=2处取得极值。
在x=2处取得极值。 的值及函数
的值及函数 的单调区间;
的单调区间; 有三个实根
有三个实根 求证:
求证:
 粤公网安备 44130202000953号
粤公网安备 44130202000953号