在平面直角坐标系中,若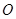 为坐标原点,则
为坐标原点,则 、
、 、
、 三点在同一直线上的充要条件为存在唯一的实数
三点在同一直线上的充要条件为存在唯一的实数 ,使得
,使得 成立,此时称实数
成立,此时称实数 为“向量
为“向量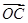 关于
关于 和
和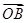 的终点共线分解系数”.若已知
的终点共线分解系数”.若已知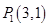 、
、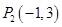 ,且向量
,且向量 是直线
是直线 的法向量,则“向量
的法向量,则“向量 关于
关于 和
和 的终点共线分解系数”为 .
的终点共线分解系数”为 .
推荐套卷
在平面直角坐标系中,若 为坐标原点,则
为坐标原点,则 、
、 、
、 三点在同一直线上的充要条件为存在唯一的实数
三点在同一直线上的充要条件为存在唯一的实数 ,使得
,使得 成立,此时称实数
成立,此时称实数 为“向量
为“向量 关于
关于 和
和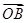 的终点共线分解系数”.若已知
的终点共线分解系数”.若已知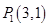 、
、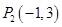 ,且向量
,且向量 是直线
是直线 的法向量,则“向量
的法向量,则“向量 关于
关于 和
和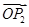 的终点共线分解系数”为 .
的终点共线分解系数”为 .