.（本小题满分14分）
已知圆M：
及定点
，点P是圆M上的动点，点Q在NP上，点G在MP上，且满足
（1）求点G的轨迹C的方程；
（2）过点K（2，0）作直线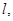
与曲线C交于A、B两点，O是坐标原点，设
是否存在这样的直线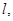使四边形OASB的对角线相等？若存在，求出直线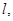的方程；若不存在，说明理由.
相关试题
的终边的范围,并由此写出角
;(2)cos
.
是第二象限的角，试分别确定2
,
+
)=-
,且
(n∈Z).
+k
)=-2cos(
;
sin2
cos2
+cos
,
).求值：推荐套卷
.（本小题满分14分）
已知圆M：及定点，点P是圆M上的动点，点Q在NP上，点G在MP上，且满足
（1）求点G的轨迹C的方程；
（2）过点K（2，0）作直线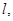与曲线C交于A、B两点，O是坐标原点，设是否存在这样的直线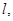使四边形OASB的对角线相等？若存在，求出直线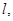的方程；若不存在，说明理由.
粤公网安备 44130202000953号