(本题满分15分) 已知函数f (x)＝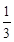
x3＋ax2＋bx， a , b
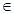R．
(Ⅰ) 曲线C：y＝f (x) 经过点P (1，2)，且曲线C在点P处的切线平行于直线y＝2x＋1，求a，b的值；
(Ⅱ) 已知f (x
)在区间 (1，2) 内存在两个极值点，求证：0＜a＋b＜2．
相关试题
，A∪B＝R，
中，
分别是
，
的中点，
是
的中点，现沿
及
三点重合，重合后的点记为
．
平面
；
的余弦值．
中，四边形
是边长为2的正方形，
，
为
上的点，且
平面
．
平面
；
的大小；
到平面
的棱长为2，点
为棱
的中点．
与平面
所成角的余弦值；
的余弦值．推荐套卷
(本题满分15分) 已知函数f (x)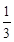＝x3＋ax2＋bx， a , b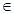R．
(Ⅰ) 曲线C：y＝f (x) 经过点P (1，2)，且曲线C在点P处的切线平行于直线y＝2x＋1，求a，b的值；
(Ⅱ) 已知f (x)在区间 (1，2) 内存在两个极值点，求证：0＜a＋b＜2．
粤公网安备 44130202000953号