在△ABC中，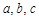
分别是内角A , B , C所对的边，若
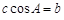， 则△ABC形状为
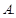一定是锐角三角形 
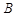. 一定是钝角三角形 
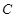. 一定是直角三角形 
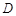. 可能是锐角三角形, 也可能是钝角三角形
相关试题
，则这四个数的大小关系是（ ）
满足约束条件
,则目标函数
的最大值为（）
，
，则A∩B=（）
=a+bi，（a，b∈R），则（a，b）为（）
，推荐套卷
在△ABC中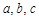，分别是内角A , B , C所对的边，若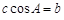， 则△ABC形状为 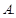一定是锐角三角形 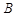. 一定是钝角三角形 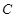. 一定是直角三角形 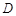. 可能是锐角三角形, 也可能是钝角三角形
粤公网安备 44130202000953号