某地政府为科技兴市,欲在如图所示的矩形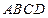 的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形
的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形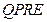 (线段
(线段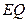 和
和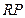 为两个底边),已知
为两个底边),已知
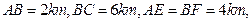 其中曲线段
其中曲线段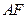 是以
是以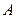 为顶点、
为顶点、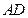 为对称轴的抛物线的一部分.分别以直线
为对称轴的抛物线的一部分.分别以直线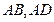 为
为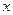 轴和
轴和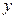 轴建立平面直角坐标系.(1)求曲线段
轴建立平面直角坐标系.(1)求曲线段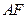 所在抛物线的方程;(2)设点
所在抛物线的方程;(2)设点 的横坐标为
的横坐标为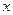 ,高科技工业园区的面积为
,高科技工业园区的面积为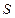 .试求
.试求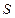 关于
关于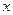 的函数表达式,并求出工业园区面积
的函数表达式,并求出工业园区面积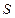 的最大值.
的最大值.
推荐套卷
某地政府为科技兴市,欲在如图所示的矩形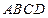 的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形
的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形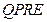 (线段
(线段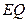 和
和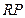 为两个底边),已知
为两个底边),已知
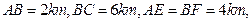 其中曲线段
其中曲线段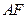 是以
是以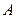 为顶点、
为顶点、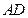 为对称轴的抛物线的一部分.分别以直线
为对称轴的抛物线的一部分.分别以直线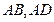 为
为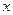 轴和
轴和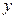 轴建立平面直角坐标系.(1)求曲线段
轴建立平面直角坐标系.(1)求曲线段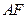 所在抛物线的方程;(2)设点
所在抛物线的方程;(2)设点 的横坐标为
的横坐标为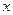 ,高科技工业园区的面积为
,高科技工业园区的面积为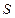 .试求
.试求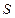 关于
关于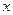 的函数表达式,并求出工业园区面积
的函数表达式,并求出工业园区面积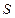 的最大值.
的最大值.