(本小题满分12分)一个袋子中有红、白、蓝三种颜色的球共24个，除颜色外完全相同，已知蓝色球3个. 若从袋子中随机取出1个球，取到红色球的概率是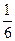
.
(1)求红色球的个数；
(2)若将这三种颜色的球分别进行编号，并将1号红色球，1号白色球，2号蓝色球和3号蓝色球这四个球装入另一个袋子中，甲乙两人先后从这个袋子中各取一个球(甲先取，取出的球不放回)，求甲取出的球的编号比乙的大的概率．
相关试题
的不等式
与
，当
为任意实数时，至少有一个桓成立。
为何值时，关于
的方程
的两根：
的图象如图所示，试判断
及
的符号。
,
，
,求证：
＜－1；
在（0，1）内有两个实根.
，设方程
的两个实数根为
和
. 
，设函数
的对称轴为
，求证：
；
，
，求
的取值范围.推荐套卷
(本小题满分12分)一个袋子中有红、白、蓝三种颜色的球共24个，除颜色外完全相同，已知蓝色球3个. 若从袋子中随机取出1个球，取到红色球的概率是.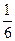
(1)求红色球的个数；
(2)若将这三种颜色的球分别进行编号，并将1号红色球，1号白色球，2号蓝色球和3号蓝色球这四个球装入另一个袋子中，甲乙两人先后从这个袋子中各取一个球(甲先取，取出的球不放回)，求甲取出的球的编号比乙的大的概率．
粤公网安备 44130202000953号