在棱长为2的正方体ABCD－A1B1C1D1中，点O为底面ABCD的中心，在正方体ABCD－A1B1C1D1内随机取一点P，则点P到点O的距离大于1的概率为（注：球的体积公式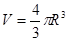
）
A． |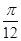
B．1－ |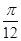
C． |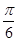
D．1－ |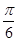
中，若
，
，则
（）
，则z为
（）
（）
的定义域是（）
相关知识点
推荐套卷
在棱长为2的正方体ABCD－A1B1C1D1中，点O为底面ABCD的中心，在正方体ABCD－A1B1C1D1内随机取一点P，则点P到点O的距离大于1的概率为（注：球的体积公式）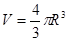
| A． |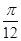
B．1－ |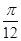
C． |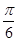
D．1－ |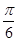
粤公网安备 44130202000953号