(本小题满分14分)
定长为3的线段AB两端点A、B分别在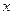 轴,
轴, 轴上滑动,M在线段AB上,且
轴上滑动,M在线段AB上,且
(1)求点M的轨迹C的方程;
(2)设过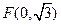 且不垂直于坐标轴的动直线
且不垂直于坐标轴的动直线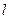 交轨迹C于A、B两点,问:线段
交轨迹C于A、B两点,问:线段 上
上
是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明。
推荐套卷
(本小题满分14分)
定长为3的线段AB两端点A、B分别在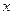 轴,
轴, 轴上滑动,M在线段AB上,且
轴上滑动,M在线段AB上,且
(1)求点M的轨迹C的方程;
(2)设过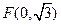 且不垂直于坐标轴的动直线
且不垂直于坐标轴的动直线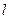 交轨迹C于A、B两点,问:线段
交轨迹C于A、B两点,问:线段 上
上
是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明。